


هيبياس الأثيني
5 معلومات شهيرة كاذبة: أينشتاين فاشل في الرياضيات.. ونابليون كان قصير القامة | قوائم في دقائق
القصة المذكورة أسطورة. لكن السر الذي كشفه بطلها هيبياس الأثيني حقيقي.. سر مثّل خطرًا على معتقدات الذين عاشوا تلك الفترة؛ لذا قرر أئمة مدرسة فيثاغورس الرياضية أن يبقوه مدفونًا بينهم.
في حدود القرن السادس قبل الميلاد، تملك الرياضيون الأوائل هوسًا بأهمية الأعداد الصحيحة ونسبها (1، 2، 3). اعتبروا أنها سر خلق الكون، حتى أن فيثاغورس كتب فوق مدرسته “كل شيء رقم”!
تمتّعت النظرية بأهمية كبيرة بين أتباع فيثاغورس حتى توصلوا إلى سرٍّ مُرعب، قرروا منْع ظهوره للعلن بأي ثمن.
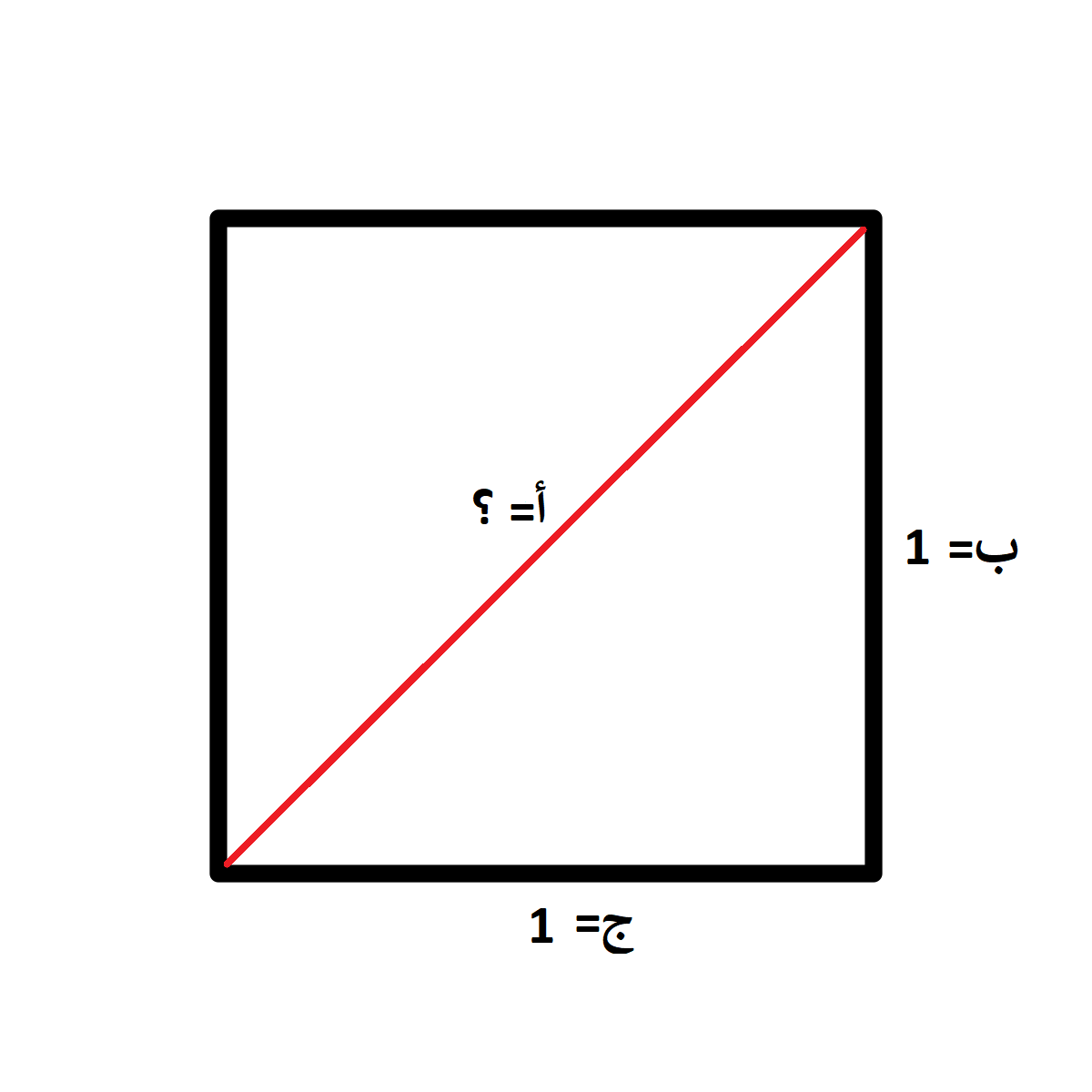
اعتقد الفيثاغورسيون أن الإجابة سهلة، اعتمادًا على نظرية “المثلثات” التي شرح بها أستاذهم كيفية حساب أطوال أضلاع مثلث قائم الزاوية: “أن مجموع مربعي طولي ضلعي الزاوية القائمة مساوٍ لمربع طول الوتر المقابل لهما”، والتي يُمكن التعبير عنها بهذه المعادلة
(أ تربيع= ب تربيع+ج تربيع).
5 ردود على فرضية حلمي بكر.. هل كانت الموسيقى الفرعونية أفريقية الأصل؟| أمجد جمال
حسنًا. هذا هو الحل الرياضي، فأين المشكلة؟
المشكلة أن هذا الرقم لا يُمكن تحديده بنسبة منطقية تشبه تلك التي نحصل عليها خلال التعامل مع أرقام صحيحة، مثل 2/3 الذي يُمكن التعبير عنها بسهولة بالرقم 1.5.
بذل الفيثاغورسيون جهودًا كبيرة لتحديد الناتج، واستمر الفشل، ليكتشفوا لأول مرة وجود نسب رياضية لا يُمكن التعبير عنها بأرقام صحيحة، في ضربة موجعة لقناعتهم بأن كافة الأرقام دقيقة يُمكن تمثيلها جميعًا بنسب صحيحة.
اعتقد فيثاغورس أن هذه الأرقام غير المنطقية “خطأ كوني” يجب إبقاؤه سرًّا، وهو النهج الذي سار عليه أتباعه من بعده.
بعد قرنٍ، كشف فيلسوف الرياضيات هيبياس الحقيقة للعالم: الأرقام كلها ليست كاملة كما روّج الفيثاغورسيون، بل يضم العالم أرقامًا “غير منطقية” أو غير نسبية، مثل (2√) وغيره من القيم صعبة التحديد.
هنا يأتي دور الأسطورة: عاقب الفيثاغوريون هيبياس بالقتل غرقًا لكشفه سر الـ(2√).
وبخلاف هذا الرقم، عرفت الرياضيات أرقامًا غير منطقية أخرى، مثل حاصل قسمة 7/22، والذي يُساوي 3.1415926535897932384626433832795. هذه القيمة العشرية تستمر بلا توقف، دون أن نستطيع اختزالها في قيمة عددية ثابتة، لذا من المستحيل التعبير عن حاصل قسمة 7/22 برقم صحيح، فمنحها علماء الرياضيات الاسم الكودي “باي – pi”، الذي رُمِز له بالعلامة “π”. ويطلق عليه في اللغة العربية “ط”
ومن بين سلسلة الأرقام “غير المنطقية”، حمل أحدها شهرة عالمية، نعرفه اليوم بالنسبة الذهبية.
ألان تورنج.. عبقري الحرب العالمية الثانية المنسي والمثلي المنتحر
نحو عام 300 ق.م، طرح إقليدس في كتابه “العناصر”، أول تعريف لـ”النسبة الذهبية”.
تساوي النسبة الذهبية – تحديدًا – نصف مجموع 1 والجذر التربيعي للرقم =5 ((1 + √5)/2)، وهو ما يُعطينا رقمًا تقريبًا هو 1.61803398874989484820 (إلخ…).
هذا الرقم يمتدُّ بلا نهاية كما هي عادة الأرقام غير المنطقية.
لتوضيح هذه النسبة رياضيًا، لنتخيّل أن أمامك خط مستقيم هو (أ-ب)، وضعنا عند أحد أجزاء هذا الخط النقطة (ج).
أ_______________ج_______ب
إذا أردنا تقسيم هذا الخط وفق النسبة الذهبية يجب أن يخضع لمعادلة (أ ج / ج ب= أ ب / أ ج)، أي أن النسبة بين المسافة الأولى أ ج والمسافة الثانية ج ب = النسبة بين المسافة الكلية أ ب والمسافة أ ج.
بمعادلة رياضية: ناتج الجزء الطويل (أ-ج) مقسومًا على الجزء القصير (ج-ب) = الطول الكامل (أ-ب) مقسومًا على الجزء الطويل (أ-ج)
وهو ما يساوي في النهاية رقم 1.618.
اعتقد الإغريق أن الاعتماد على هذه المعادلة في تصميم الأشكال الهندسية يجعلها أكثر جمالًا، فاعتمدوا عليها بإفراط في تصميم الكثير من منجزاتهم الإبداعية.
الثقوب السوداء بطل نوبل الفيزياء 2020.. ما توقعه أينشتاين لكنه رفض تصديق وجوده | فادي داوود
تقول بريا هيمينواي في كتابها “النسبة الإلهية: فاي في الفن والطبيعة والعلوم”: “إن النحات اليوناني فيدياس استخدم النسبة الذهبية في تصميم أشهر منحوتاته داخل معبد البارثينون وعند تصميم تمثال زيوس، أحد عجائب العالم السبعة.”
لذا، أطلق عالم الرياضيات الأمريكي مارك بار اسم “فـٰي – phi” (ϕ) على النسبة الذهبية عام 1910، وهو أول حرف في اسم فيدياس Phidias، بدلًا من رمزها السابق تاو (τ) وهو الحرف الأول من كلمة (τομή) اليونانية القديمة التي تعني قطعة أو قِسم.
بعض الدراسات أكدت أن معبد الإله أبولو الإغريقي أُنشئ، أيضًا، وفقًا لأبعاد النسبة الذهبية.
وفي العصور الحديثة، ظهرت النسبة الذهبية في لوحات ليوناردو دا فنشي وسلفاردو دالي.
وفقًا للعديد من المصادر، فإنك إن رسمتَ مستطيلًا حول وجه “موناليزا” ليوناردو دا فينشي، فإن نسبة ارتفاع هذا المستطيل إلى عرضه تساوي النسبة الذهبية.

النسبة الذهبية في الموناليزا
لا يُمكننا التأكد من حقيقة استخدام دافنشي النسبة الذهبية لرسم لوحته الأشهر. لكن يجب مراعاة حقيقة أن دافنشي كان صديقًا لعالم الرياضيات الإيطالي لوكا باتشولي، الذي نشر كتابًا عنها عام 1509 بعنوان “التناسب الإلهي”، احتوى على رسوم توضيحية رسمها دافنشي بنفسه.
أما فيما يتعلّق بلوحة سلفادور دالي، فإن أبعاد لوحته الشهيرة “سر العشاء الأخير”، تساوي النسبة الذهبية.

النسبة الذهبية في لوحة سر العشاء الأخير
10 قصص محكية عن النبي موسى .. أين الحقيقة وأين الأسطورة؟ | الحكاية في دقائق
يرى كثيرون أن النسبة الذهبية ممتعة جماليًا؛ لأنها شائعة أصلًا في الطبيعة من حولنا، مثل نسبة صَدَفة الحلزونية لحيوان Nautilus (أو البحار كما كان يُطلق عليه في اللغة اليونانية القديمة). أو ربما في نمو بعض أوراق الأشجار وحركة نبات عباد الشمس بأنماط قريبة من تلك النسبة، بل ويتكرر هذا النمط الحلزوني في أشكال الأعاصير وحتى المجرات نفسها كمجرتنا درب التبانة!

النسبة الذهبية في صدفة نوتيلوس
وفي دراسة، نُشرت 2019، أكد باحثون من جامعة جونز هوبكنز، أن أبعاد الجمجمة البشرية تتبع النسبة الذهبية.
أينما نظرت إلى قلب الظواهر الطبيعية المعقدة، بطريقة أو بأخرى، تظهر لك النسبة الذهبية بصورة مفاجأة وغير متوقعة. قد يكون الكون فوضويًا ولا يمكن التنبؤ به، لكنه يظل أيضًا عالمًا ماديًا منظمًا للغاية وملزمًا بقوانين الرياضيات، وربما كانت النسبة الذهبية هي الشكل الأكثر جمالًا لإظهار تلك القوانين.
أو ربما كانت تلك طريقتنا كبشر للبحث عن الجمال والتناغم والتناسق وسط الفوضى.
الرجل غير المنطقي (Cambridge Maths)
هيبياس الأثيني (Encyclopedia)
فيثاغورس.. سيرة ذاتية (Story of Mathematics)
علم الجمال والنسبة الذهبية (Plus.Maths)
النسبة الذهبية في الرياضيات (Britannica)
اكتشف الطرق التي استخدم بها ليوناردو دافنشي النسبة الذهبية في بعض أشهر أعماله الفنية (متحف العلوم)
مقدمة عن النسبة الذهبية (أدوبي)
وثيقة تصميم شعار بيبسي (ARNELL GROUP)
تصميم هرم خوفو الأكبر (Springer)
أبعاد جمجمة الثدييات والنسبة الذهبية (دراسة جامعة جونز هوبكنز)
Book: The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number, by Mario Livio.
Book: Divine Proportion: Phi In Art, Nature, and Science, by Priya Hemenway.
 موضوعات متعلقة
موضوعات متعلقة